Descriptive statistics of the time series

Descriptive statistics and basement levels assesment

In this step, a set of descriptive statistics is computed for every time series. These statistics do not take into account the time and thus all the concentration points are considered to be equivalent - the time series reduces to common dataset, which can be easily described by its central tendency and spread (variance).
If these two quantities do not significantly change in time (stationarity), they could be used as a descriptors of basement levels of the pollution (average concentrations of pollutant and a magnitude of its fluctuations).
Nevetheless, if the central tendency and spread decreases or increases in time (look at the plots), these quantities are meaningless and it is necesary to estimate increase or decrease by time trends (see the next step).

A culmination of the whole analysis consist of two last steps: computing a table of overall descriptive statistics and simple test results containing estimates of pollution basement levels, variance of the measurements and their progress in time (i.e. trend analysis). Of course, the statistical significance of tests is of the highest importance, showing, whether the results can be used as tools for description of the processes in the area of monitoring.

In this step, (stationary) descriptive statistics are computed. Sometimes, the mean could be the best option to estimate the average concentration, but also an information on the spread within the year is of interest. Otherwise the geometric mean describes better the central value or it is more suitable to deploy the median. There are several methods for estimation of all these statistics in our example. There are three types of statistics in all of them: parametric for normal and lognormal distribution (mean and standard deviation in arithmetic and geometric variant) and nonparametric (median and min & max) for a universal use.

 

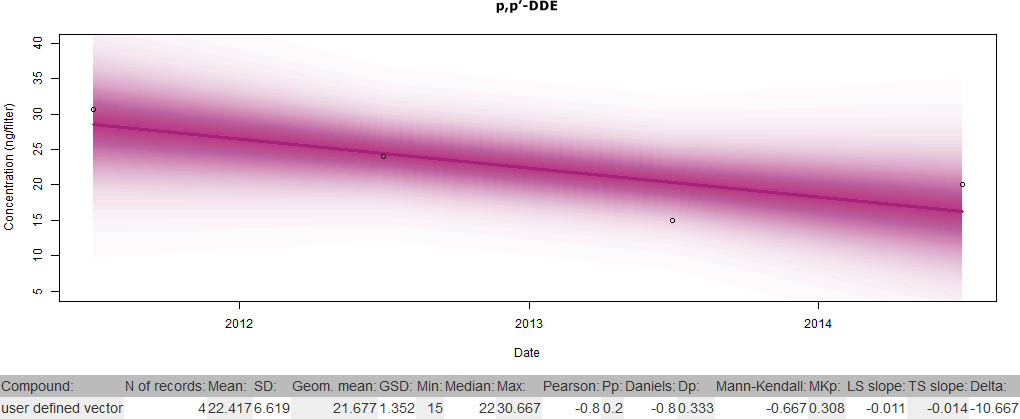
Descriptive statistics

There are lots of statistics applicable when describing the time series (either aggregated or with the primary data - try the difference in the example below):

Number of samples

This value represents the overall number of valid records used to calculation of further statistics.

Mean

Standard deviation

Geometric mean

Geometric standard deviation

Minimum

Median

Maximum

Previous step.

References

Sen, P. K., Estimates of the Regression Coefficient Based on Kendall's Tau. Journal of the American Statistical Association 1968, 63 (324), 1379-1389.

 Next step
7: Descriptive statistics
7: Descriptive statistics